Blog – Dusza inżyniera

Charakterystyki częstotliwościowe – cz. I (bez wzorów)

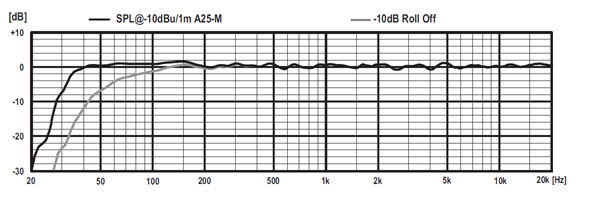
Charakterystyka częstotliwościowa, charakterystyka Bodego – to brzmi dumnie (i skomplikowanie). W rzeczywistości każdy ma szansę się z nimi zapoznać, jeśli np. kupuje słuchawki, głośniki, mikrofon (lub zagłębia się w dokumentację techniczną smartfona, która takie charakterystyki zawiera). W związku z tym, nawet jeśli nie mamy zamiaru wyznaczać takich charakterystyk, to warto wiedzieć, co one sobą przedstawiają i jak je interpretować. Spójrzmy np. na charakterystykę głośnika, przedstawioną na Rys. 1.

Rys. 1 Charakterystyka amplitudowa głośnika z dokumentacji dostępnej pod adresem
http://downloads.psiaudio.com/studio-monitors/PSI_A25_MS_techdata.pdf

Każdy punkt charakterystyki przedstawia informację o tym, jak układ (w tym przypadku, głośnik) przenosi drgania o określonej częstotliwości, pojawiające się na jego wejściu. Skąd się biorą drgania? Każdy dźwięk jest złożeniem drgań powietrza (a właściwie ośrodka, w którym się roznosi) o różnej częstotliwości. Nagrywamy dźwięk, przekształcając w mikrofonie falę akustyczną na natężenie prądu – a następnie, podczas odtwarzania, ma miejsce odwrotny proces. Gdyby założyć, że nagrywanie oraz przesył sygnału są idealne, to moglibyśmy mówić, że charakterystyka pokazuje, czy dźwięk pochodzący z głośnika jest zniekształcony w stosunku do oryginału, czy też nie. Jest to maksymalne uproszczenie problemu, ale oddające ideę charakterystyki. (W rzeczywistości, na wejściu układu jest prąd elektryczny, więc charakterystyka może co najwyżej przedstawiać, jak dokładnie układ odwzorowuje już nagrany dźwięk, który może być częściowo zniekształcony przez mikrofon – jego charakterystyka pojawi się za chwilę – a do tego dochodzi jeszcze wpływ charakterystyk wzmacniacza oraz kabla, którym łączymy wzmacniacz z głośnikiem. Trzeba jeszcze zauważyć, że układ jest nieliniowy, co dodatkowo utrudnia analizę – ale po co ja to komplikuję?). Zostańmy przy tym maksymalnym uproszczeniu.

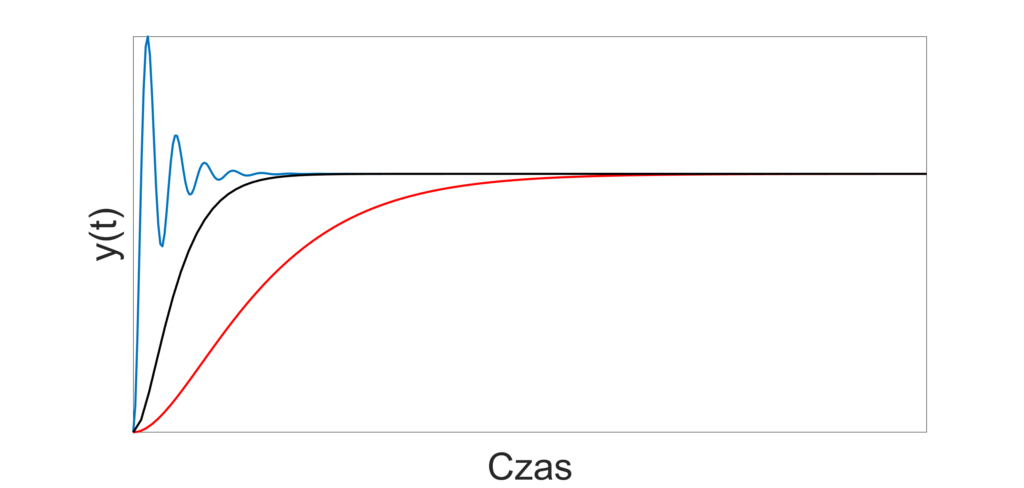
Przedstawiona na Rys. 1 charakterystyka jest charakterystyką amplitudową. Pokazuje, jak zmienia się amplituda drgań na wyjściu układu, w porównaniu do amplitudy drgań na wejściu. Zwykle stosuje się skalę logarytmiczną dlatego wartość „0 dB” na charakterystyce odpowiada dokładnemu przenoszeniu drgań (amplitudy drgań na wyjściu i na wejściu są identyczne, więc ich stosunek równy jest jedności – a log(1)=0). Widzimy więc, że układ, którego charakterystyka została przedstawiona na Rys. 1 kolorem czarnym, przenosi drgania w zakresie od mniej więcej 40 Hz do 20 kHz (na tej wartości kończy się charakterystyka na rysunku – w rzeczywistości to pasmo jest nieco szersze). Ponieważ zakres częstotliwości, które słyszymy, mieści się (dla przeciętnego człowieka) w zakresie ok 16 Hz – 20 (niektórzy podają 22) kHz, to można przyjąć, że z takiego głośnika powinniśmy być zadowoleni (a dla głębokich basów trzeba będzie coś dokupić).

Przy okazji, proszę zwrócić uwagę na to, że oś pozioma również jest w skali logarytmicznej (logarytm o podstawie 10 – odległość pomiędzy 10 a 100 jest taka sama jak między 100 a 1000).

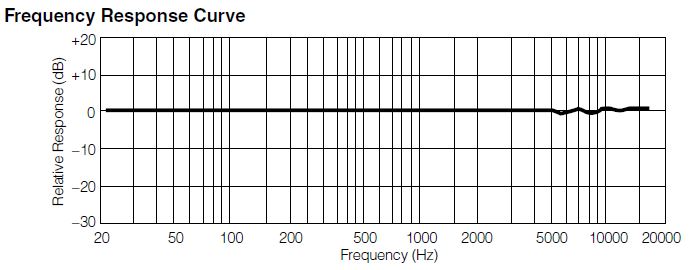
Podobnie można przedstawić charakterystyki mikrofonu. na Rys. 2 i 3 można zobaczyć charakterystyki dwóch różnych mikrofonów, o różnym przeznaczeniu. Pierwszy z nich (Rys. 2), jest przykładem typowego mikrofonu estradowego. Dźwięki o charakterystyce poniżej 100 Hz są tłumione (charakterystyka poniżej linii „0”), przy czym tłumienie jest tym większe, im niższa częstotliwość. Pozwala to m.in. na wytłumienia drgań, mających swe źródło w zasilaniu różnych urządzeń prądem zmiennym (50 Hz) oraz w drganiach sceny. W zakresie 100 Hz-2kHz charakterystyka jest płaska, wartości w okolicach 0 (skala logarytmiczna – czyli drgania sa przenoszone), co pozwala na wyłapanie dużej części wokalu. W zakresie 2kHz-10kHz wokal jest wzmacniany, by mógł się przebić przez dźwięki, pochodzące z instrumentów, które w przeciwnym wypadku „przykryłyby” go (pamiętajmy jednak, że jeśli chcielibyśmy dokładniej się temu przyjrzeć, należałoby jeszcze uwzględnić charakterystyki kabli i głośników). Z kolei mikrofon o charakterystyce przedstawionej na Rys. 3 w identyczny sposób przenosi wszystkie dźwięki do ok. 16kHz, zapewniając ich wierne odwzorowanie na nagraniu.

Rys. 2 Charakterystyka mikrofonu, wzmacniającego pewne częstotliwości

Rys. 3 Charakterystyka mikrofonu, przenoszącego dźwięki w niemal całym zakresie słyszalności

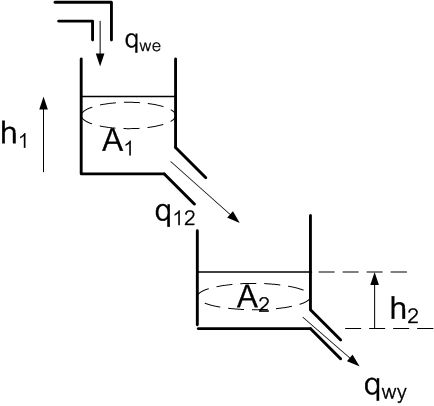
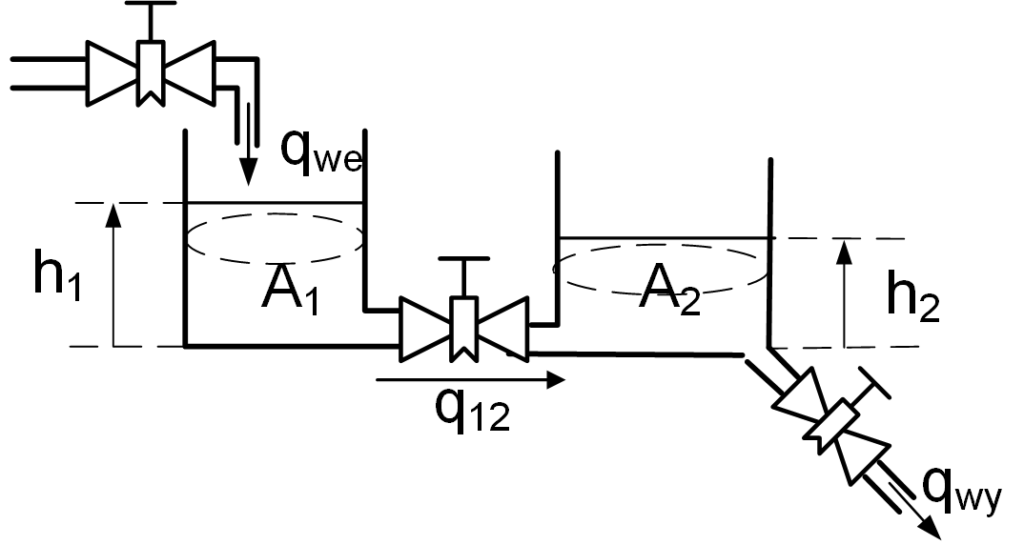
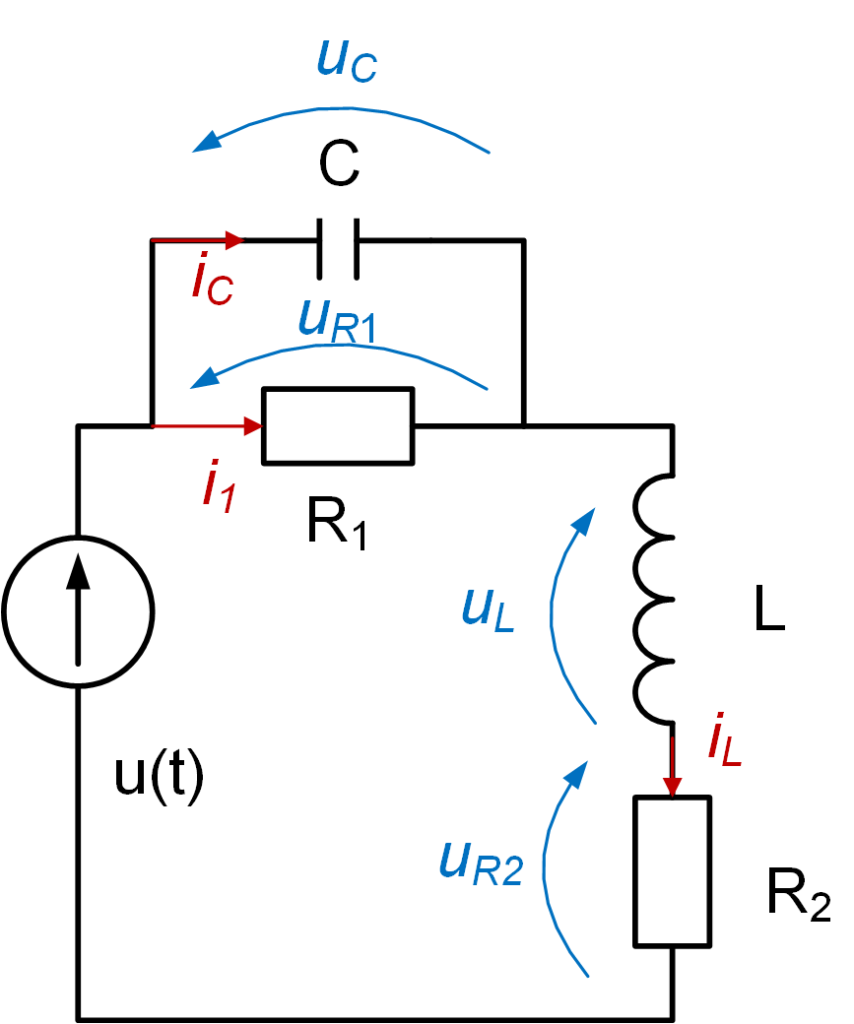
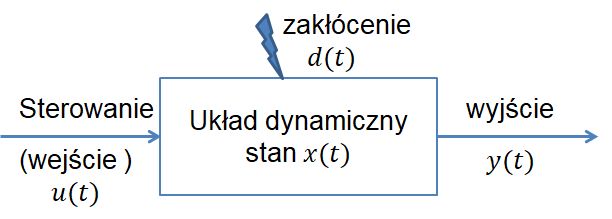
Ale nie tylko w urządzeniach audio charakterystyki częstotliwościowe mają znaczenie. Wyobraźmy sobie dwa taśmociągi i robota między nimi, którego zadaniem jest przekładanie elementów z jednego taśmociągu na drugi (Rys. 4).

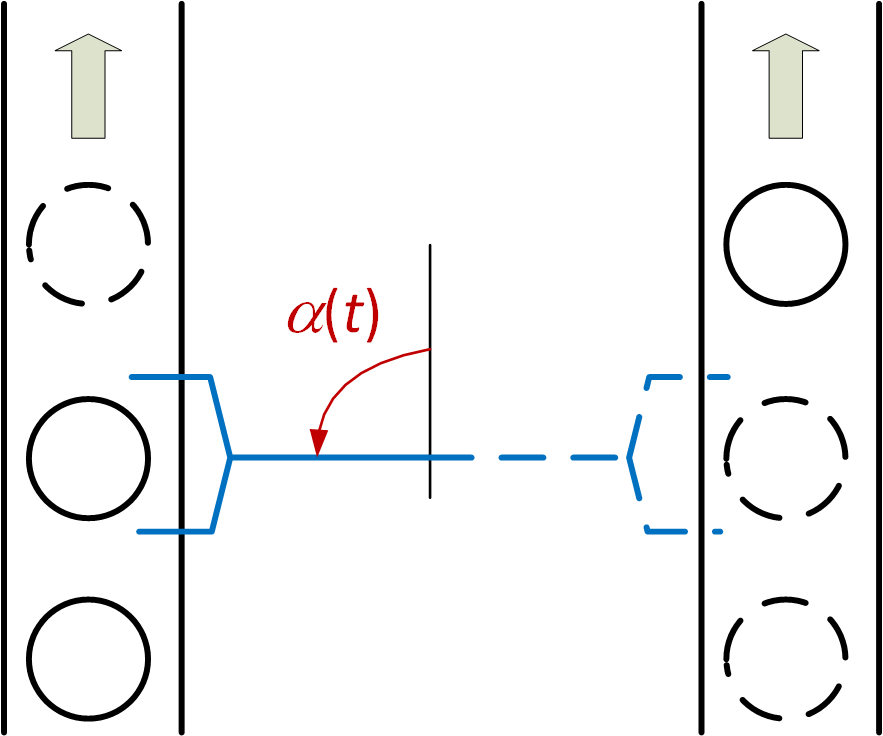
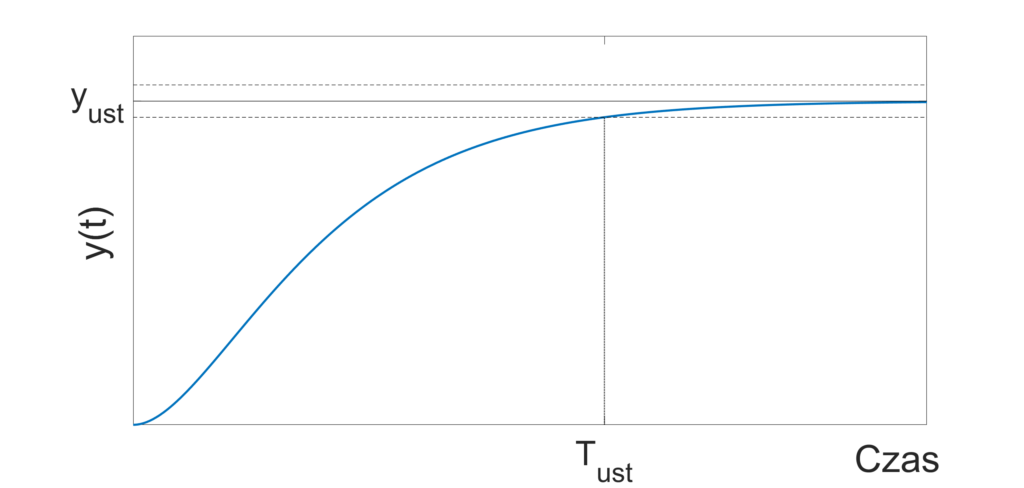
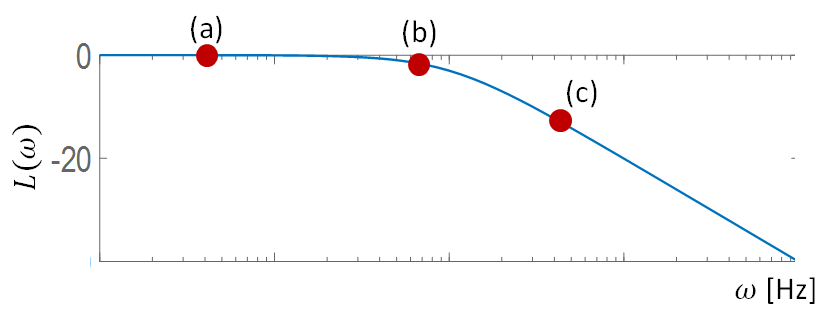
Rys. 4 Układ, w którym robot przekłada elementy z jednej strony na drugą

Jedno z założeń projektowych może dotyczyć szybkości przesuwania taśmociągów – czy robot zdąży przełożyć element z jednej strony na drugą? Odpowiedzi na to pytanie może dostarczyć charakterystyka amplitudowa ramienia robota. Na Rys. 5 zaznaczono trzy punkty. Jeśli będziemy zmieniać sterowanie silnika, obracającego ramię robota niezbyt szybko (punkt (a)), to bez najmniejszych problemów robot zdąży przenieść elementy z jednego taśmociągu na drugi (Rys. 5a). Jeśli zwiększymy częstotliwość zmian (punkt (b)), to co prawda ramię robota zdąży obrócić się z jednego zadanego położenia w drugie, ale najprawdopodobniej nie zdąży złapać i upuścić elementów (Rys. 5b). Jeśli jeszcze bardziej zwiększymy częstotliwość zmian zadanego położenia (a co za tym idzie, częstotliwość sygnału sterującego silnikiem – punkt (c)), to położenie ramienia robota będzie oscylować – trochę w lewo, trochę w prawo, ale nigdy nie dojdzie do zadanego (Rys. 5c).

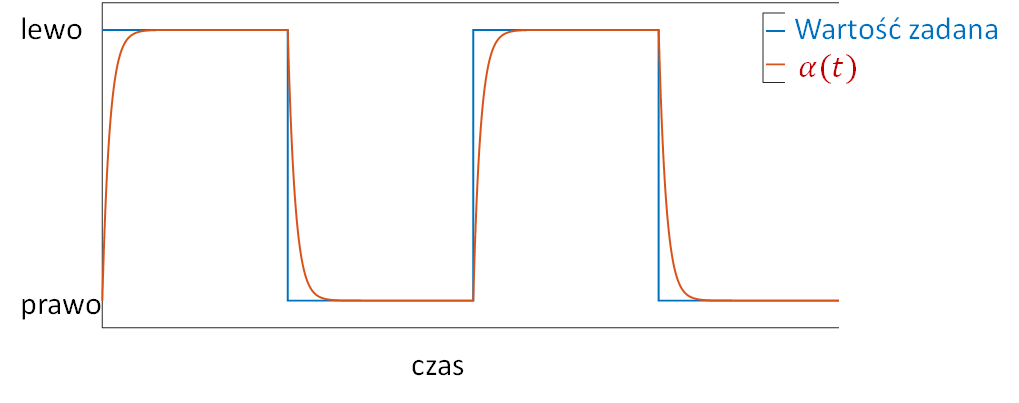
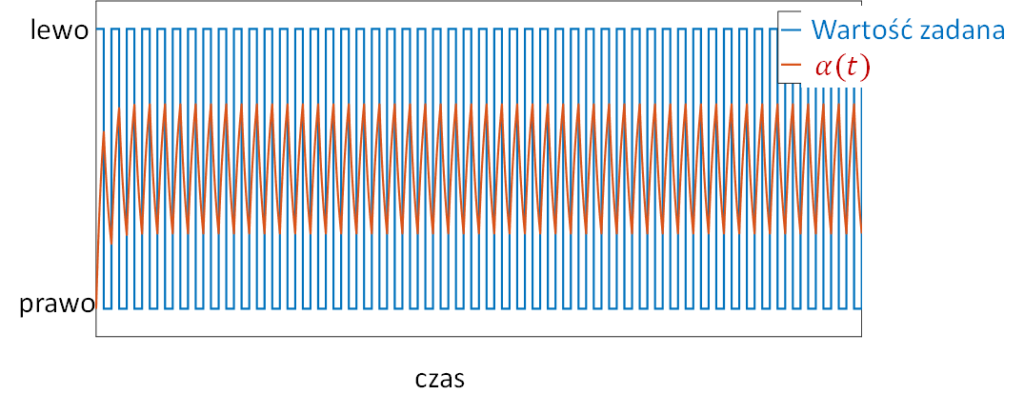
Rys. 5 Przykładowa charakterystyka robota

Jeśli sygnałem wejściowym jest zakłócenie, to interpretacja charakterystyki amplitudowej jest identyczna – mówi, jakie zakłócenia są przez układ przenoszone, jakie wzmacniane, a jakie tłumione.

Wiemy już, jak interpretować charakterystyki amplitudowe. Skąd one się biorą? Z dwóch źródeł. Po pierwsze, na etapie projektowania układu określamy, jak, z punktu widzenia przeznaczenia naszego układu, powinna wyglądać charakterystyka – trzeba ją więc umieć obliczyć (i o tym w kolejnym wpisie). Należy jednak pamiętać, że przy wyznaczaniu charakterystyk zazwyczaj mocno upraszczamy opis matematyczny układu. Dlatego charakterystyki, jak pokazane na Rys. 1-3, są wyznaczane eksperymentalnie – mierzymy amplitudę drgań wyjściowych układu pobudzanego drganiami o określonej częstotliwości i zaznaczamy punkt na charakterystyce. A potem zmieniamy częstotliwość drgań na wejściu i znajdujemy kolejny punkt charakterystyki… pamiętając (kto może) o ograniczeniach metody w przypadku układów nieliniowych (kiedyś dojdę do wpisu na ten temat).

Jeśli wpis Ci się spodobał i uważasz, że może warto, by Twoi znajomi go przeczytali – proszę poleć go.

Transmitancja (porządkujemy opis, cz. I)

Poprzednie wpisy pokazały, że opis układów dynamicznych przyjmuje postać układu równań różniczkowych i algebraicznych. Jeśli interesuje nas odpowiedź układu (czyli zmiany w czasie wielkości, które ten układ charakteryzują, np. napięcia, prędkości, położenia itd.) na zadane wymuszenie, należałoby te równania rozwiązać. Można się jednak przy tym mocno spocić. Od czegóż jednak jedna z ważnych umiejętności człowieka – umiejętność wykorzystania czegoś, co już zrobił ktoś inny?

Trudno jednak przypuszczać, by każdy układ, z którym się spotkamy, był już dokładnie przez kogoś przeanalizowany (choć, oczywiście, przykłady przywoływane w moich wpisach były już na wszelkie możliwe sposoby analizowane, i to wielokrotnie, przez wiele różnych osób). Wielu matematyków poświęciło lata pracy na rozwiązywanie równań, w których pojawiały się tajemnicze parametry, i dostarczyło nam gotowych narzędzi. Trzeba jednak zdawać sobie sprawę z tego, że narzędzia te wymagają uporządkowania opisu matematycznego modelu. Każdy ze wspomnianych matematyków zaczynał bowiem od mniej więcej takiego stwierdzenia: „Załóżmy, że równanie przyjmuje następującą postać …”. Tak więc, zanim zaczniemy korzystać z owoców ich pracy, musimy przekształcić opis matematyczny do jednej ze standardowych postaci (stosując, jak to w podręcznikach często jest zapisane, „proste przekształcenia”).

Pamiętając o tym, że (przynajmniej na razie) zajmujemy się stacjonarnymi układami liniowymi (czyli opisanymi liniowymi równaniami różniczkowymi o stałych parametrach), do wyboru mamy trzy typy takiego standardowego opisu:

pojedyncze równanie różniczkowe (w bieżącym wpisie pojawi się tylko, raz ponieważ (chyba) dużo wygodniej jest posługiwać się dwoma pozostałymi typami)
transmitancja operatorowa (w tym wpisie – dla układów o jednym wejściu i jednym wyjściu);
liniowe równania stanu i wyjścia (tymi zajmę się w osobnym wpisie).

Oprócz tego, że przedstawienie opisu układu w ustandaryzowanej postaci pozwala skorzystać z rozwiązań, wyprowadzonych wcześniej dla „przypadków ogólnych”, jest ono niezbędne, jeśli chcemy wykorzystać oprogramowanie do symulacji lub analizy własności danego układu (bo dane wejściowe, wprowadzane do jakiegokolwiek programu powinny mieć określoną strukturę, ustaloną na etapie pisania kodu tego programu).

Przyjrzyjmy się pierwszemu z przykładów mechanicznych, przedstawionemu we wcześniejszym wpisie (Rys. 1).

Jest on opisany następującym równaniem:

$\begin{equation*}M \ddot x = F-K \cdot x-D \cdot \dot x.\end{equation*}$

Jeśli uporządkujemy opis w taki sposób, by zmienna opisująca położenie masy (i jej pochodne) znalazły się z jednej strony równania, a wymuszenie z drugiej:

$\begin{equation*}M \ddot x +D \cdot \dot x + K \cdot x= F,\end{equation*}$

to taki opis będzie pasował do ustandaryzowanego, pojedynczego równania różniczkowego w ogólnej postaci:

$\begin{align*}a_n x^{(n)} + a_{n-1} x^{(n-1)}+ \ldots + a_1 \dot x + a_0 x=\\=b_m u^{(m)} + b_{m-1} u^{(m-1)}+ \ldots + b_1 \dot u + b_0 u,\end{align*}$

gdzie $x^{(n)}=\frac{d^nx}{dt^n}$ oznacza pochodną funkcji $x(t)$ rzędu $n$ . Jeśli założymy powyższą postać ogólną, to w celu zdefiniowania układu wystarczy określić współczynniki $a_n, \ldots, a_0$ i $b_m, \ldots, b_0$ . W odpowiednio skonstruowanym interfejsie użytkownika programu, umożliwiającego symulację układów dynamicznych, wprowadzenie danych ([M D K], [1]) jednoznacznie pozwoli zdefiniować nasz układ mechaniczny (trzy elementy w pierwszym nawiasie oznaczają, że są trzy współczynniki równania z lewej strony, odpowiednio M, D i K, dla kolejnych pochodnych, coraz niższego rzędu, a 1 w drugim nawiasie oznacza, że wejście mnożone jest przez jeden). Jednocześnie, możemy otworzyć podręcznik do równań różniczkowych, gdzie znajdziemy sposób rozwiązania takiego równania, a dla pewnych, określonych postaci funkcji $F(t)$ – nawet gotowe rozwiązanie.

Najczęściej jednak układ taki zostanie przedstawiony w postaci tzw. transmitancji operatorowej, opisującej w ustandaryzowany sposób zależność pomiędzy wejściem a wyjściem układu (korzyści takiego podejścia zostaną przedstawione w kolejnych wpisach). Możemy posługiwać się wtedy prostym schematem zastępczym, reprezentującym układ, przedstawionym na Rys. 2:

Rys. 2 Blok transmitancji

W celu wyznaczenia transmitancji należy dokonać transformacji Laplace’a równań opisujących dynamikę układu, a następnie odpowiednich przekształceń algebraicznych. Ponieważ transmitancja ma przedstawiać sobą zależność wyjścia od wejścia, a nie od warunków początkowych, podczas transformacji Laplace’a zakłada się zerowe warunki początkowe w układzie (co z tego wynika – w odrębnym wpisie).

Zakładając, że we wspomnianym układzie mechanicznym wyjściem jest położenie, czyli $y=x$ (wcale tak być nie musi – moglibyśmy być zainteresowani np. prędkością i wtedy $y=\dot x$ )

$\begin{equation*}Ms^2 X(s)+ Ds X(s)+ KX(s)=F(s)$ \end{equation*}$

gdzie $X(s)=\mathcal{L}\left\{ x(t) \right\}$ i $F(s)=\mathcal{L}\left\{ F(t) \right\}$ oznaczają transformaty Laplace’a, odpowiednio, funkcji $x(t)$ i $F(t)$ (dla niewtajemniczonych – podczas transformacji Laplace’a zastępujemy pochodne rzędu $k$ mnożeniem przez $s^k$ ). Po uporządkowaniu otrzymujemy

$\begin{equation*}K(s)=\frac{X(s)}{F(s)}=\frac{1}{Ms^2+Ds+K}.\end{equation*}$

Jeśli interesowałaby nas prędkość masy, a nie jej położenie, wtedy wyjściem byłoby $v(t)$ . Transmitancję $K^*(s)=\frac{V(s)}{F(s)}$ można wyznaczyć albo przekształcając równanie opisujące dynamikę układu, tak by zmienną w nim było $v(t)$ , a nie $x(t)$ , albo korzystając z zależności pomiędzy tymi zmiennymi. Ponieważ $v(t)=\dot x(t)$ , $V(s)=\mathcal{L} \{v(t)\}=sX(s)$ (znów pomijamy warunek początkowy $x(0)$ ), czyli

(1) $\begin{equation*}K^*(s)=\frac{V(s)}{F(s)}=\frac{X(s)}{F(s)} \cdot \frac{V(s)}{X(s)}=\frac{s}{Ms^2+Ds+K}.\end{equation*}$

Zauważmy, że:

Ten sam układ fizyczny można przedstawić za pomocą różnych transmitancji, w zależności od tego, co jest jego wyjściem.
Mianownik tych transmitancji jest taki sam (a, bardziej precyzyjnie, ma takie same miejsca zerowe).
Transmitancja ma postać ułamka, w którym zarówno licznik, jak i mianownik są wielomianami, a współczynnikami tych wielomianów są liczby lub wyrażenia zawierające parametry układu (przy okazji – w modelach rzeczywistych układów fizycznych stopień wielomianu w liczniku zawsze jest mniejszy lub równy stopniowi wielomianu w mianowniku). Można, co prawda, wskazać układy, których transmitancja zawiera nie tylko wielomiany (np. nieskończeniewymiarowy podsystem modelu sterowanego systemu masowej obsługi), ale na razie o tak skomplikowanych układach nie będziemy mówić.

Najtrudniejsze (w sensie – jak odpowiedzieć, żeby pytającego usatysfakcjonować) pytanie – a co to takiego to „s”?

Odpowiedź jest w zasadzie prosta – to zmienna pomocnicza, która odpowiada zmiennej $t$ w dziedzinie czasu… Tylko, że taka odpowiedź nikogo nie satysfakcjonuje… Może kolejne wpisy pokażą, do czego ta zmienna może się przydać (każdy może sobie wyobrazić, co to znaczy $t=5$ [sekund], ale niekoniecznie, co to znaczy, że $s=2+3j$ ). Zachęcam do śledzenia dalszych wpisów. Na razie powinno wystarczyć, że $s$ to magiczny symbol, który pojawił się w wyniku zastosowania transformacji Laplace’a 🙂

Jeśli układ opisany jest większą liczbą równań, w celu wyznaczenia transmitancji należy dokonać transformacji Laplace’a wszystkich z nich. Przyjrzyjmy się układowi, przedstawionemu na Rys. 3.

Załóżmy, że przepływy są laminarne, czyli $q_{12}=C_1h_1$ i $q_{wy}=C_2h_2$ , a wyjściem jest przepływ $q_{wy}$ . Układ opisany jest równaniami (patrz wpis dotyczący opisu zbiorników)

$\begin{align*}A_1 \dot h_1 = q_{we} - q_{12}\\ \\ A_1 \dot h_2 = q_{12} - q_{wy},\end{align*}$

czyli, po uzględnieniu zależności pomiędzy przepływami a odpowiednimi poziomami cieczy

$\begin{align*}\frac{A_1}{C_1} \dot q_{12} = q_{we} - q_{12},\\ \\ \frac{A_2}{C_2} \dot q_{wy} = q_{12} - q_{wy}.\end{align*}$

Po dokonaniu transformacji Laplace’a obu równań (i założeniu zerowych warunków początkowych, o czym już w dalszych wpisach nie będę przypominał):

$\begin{align*}\frac{A_1}{C_1} s Q_{12}(s) = Q_{we}(s) - Q_{12}(s),\\ \\ \frac{A_2}{C_2} s Q_{wy}(s) = Q_{12}(s) - Q_{wy}(s).\end{align*}$

Po uporządkowaniu zapisu w każdym z równań otrzymujemy:

$\begin{align*}\left( \frac{A_1}{C_1} s +1 \right)Q_{12}(s) = Q_{we}(s),\\ \\ \left( \frac{A_2}{C_2} s +1 \right) Q_{wy}(s) = Q_{12}(s),\end{align*}$

czyli

$\begin{align*}Q_{12}(s) = \frac{1}{\frac{A_1}{C_1} s +1 }Q_{we}(s),\\ \\ Q_{wy} (s)= \frac{1}{ \frac{A_2}{C_2} s +1}Q_{12}(s).\end{align*}$

Ostatecznie

$\begin{equation*}Q_{wy} (s)= \frac{1}{ \frac{A_2}{C_2} s +1} \cdot \frac{1}{\frac{A_1}{C_1} s +1 }Q_{we}(s),\end{equation*}$

czyli

$\begin{equation*}K(s)=\frac{Q_{wy} (s)}{Q_{we}(s)}= \frac{1}{ \frac{A_2}{C_2} s +1} \cdot \frac{1}{\frac{A_1}{C_1} s +1 }.\end{equation*}$

Przy okazji, zauważmy, że $q_{12}$ , będące wyjściem z pierwszego zbiornika, jest jednocześnie wejściem do drugiego zbiornika, co można przedstawić za pomocą schematu blokowego z Rys. 4.

Rys. 4 Szeregowe połączenie dwóch układów

Jeśli, tak jak na rysunku, każdy ze zbiorników potraktujemy jako osobny układ, opisany transmitancją, to transmitancja całości (połączenia szeregowego takich układów) jest iloczynem transmitancji części składowych (Rys. 5).

Rys. 5 Transmitancja zastępcza połączenia szeregowego

Na podstawie transmitancji możemy wiele powiedzieć o zachowaniu układu – np., czy po podaniu stałego wymuszenia w odpowiedzi pojawią się oscylacje (a jeśli tak, to o jakiej częstotliwości), jak szybko układ będzie reagował na zmiany wymuszenia, czy będzie przenosił, czy tłumił drgania o określonej częstotliwości, pojawiające się na wejściu. Ponadto, biorąc pod uwagę, że

$\begin{equation*}Y(s)=K(s)U(s),\end{equation*}$

Możemy wyznaczyć odpowiedź układu na dowolne wymuszenie $u(t)$ jako

$\begin{equation*}y(t)=\mathcal{L}^{-1}\left\{ Y(s) \right\}.\end{equation*}$

No dobrze – to ostatnie akurat nie musi być takie proste. Najczęściej jednak nie potrzebujemy pełnej postaci analitycznej (czyli wzoru) funkcji $y(t)$ , ale jej cech charakterystycznych, o czym będzie w kolejnych wpisach.

Jeśli wpis Ci się spodobał i uważasz, że może warto, by Twoi znajomi go przeczytali – proszę poleć go.

Opisujemy układy – poziom I (zbiorniki)

Ostatnim typem układów, które będą służyły do ilustrowania różnych zagadnień, związanych z dynamiką układów, są układy zbiorników. Najprostszy z nich wygląda tak:

Wejściem w tym układzie jest przepływ $q_{we}$ . Zależy ono tak naprawdę od ciśnienia wejściowego i charakterystyki oraz stopnia otwarcia zaworu, ale dla uproszczenia posługiwać się będziemy właśnie przepływem. Równania dla zbiorników oparte są na bardzo prostej regule – różnica między ilością cieczy wpływającej i wypływającej ze zbiornika stanowi przyrost objętości cieczy w tym zbiorniku:

$\frac{dV}{dt}=q_{we} - q_{wy}$ .

Zakładając, że pole przekroju powierzchni zbiornika jest stałe i wynosi $A$ , otrzymujemy

$A\frac{dh}{dt}=q_{we} - q_{wy}$ .

Możemy mieć do czynienia z jednym z dwóch typów przepływów: laminarnym albo turbulentnym. W przepływie laminarnym wielkość przepływu jest proporcjonalna do ciśnienia panującego w zbiorniku, a ponieważ ciśnienie jest proporcjonalne do wysokości słupa cieczy, możemy zapisać

$q_{wy}=C \cdot h$ ,

gdzie $C$ jest współczynnikiem proporcjonalności.

W przepływie turbulentnym wielkość przepływu jest proporcjonalna do pierwiastka z ciśnienia, co można zapisać jako

$q_{wy}=\hat{C} \cdot \sqrt{h}$ .

Ostatecznie, dynamika zmian objętości cieczy/wysokości słupa cieczy/przepływu wyjściowego jest opisana za pomocą jednego równania różniczkowego i jednego równania algebraicznego. Sprowadzając ten zapis do pojedynczego równania różniczkowego, np. w przypadku przepływu turbulentnego, otrzymujemy:

$A\frac{dh}{dt}=q_{we}- \hat{C} \cdot \sqrt{h}$ .

W przypadku, gdy przekrój zbiornika nie jest stały, obliczenia nieco się komplikują. Przykładowo, gdy zbiornik ma kształt lejka:

jego objętość można obliczyć jako objętość stożka (zaniedbujemy fakt, że tak naprawdę jest to stożek ścięty), czyli

$V=\frac{1}{3}\pi r^2 h$ .

Pamiętając o tym, że $h=h(t)$ i $r=r(t)$ , oraz uwzględniając zależność $r=h\tan \alpha$ , otrzymujemy $V=\frac{1}{3}\pi \tan^2\alpha h^3$ i możemy obliczyć zmianę objętości $V$ w czasie jako

$\frac{dV}{dt}=\pi \tan^2\alpha h^2 \frac{dh}{dt}$ .

W takim razie, dynamika zmian poziomu cieczy w zbiorniku opisana jest równaniem

$\pi \tan^2\alpha h^2 \frac{dh}{dt}=q_{we}-q_{wy}$ ,

gdzie $q_{wy}$ , w zależności od typu przepływu, jest opisany jedną z wyżej podanych zależności algebraicznych.

W przypadku, gdy mamy do czynienia z dwoma połączonymi zbiornikami, jak na rysunku poniżej, przepływ pomiędzy nimi zależy od różnicy ciśnień (co sprowadza się do zależności od różnicy poziomów cieczy).

Rys. 3 Układ dwóch połączonych zbiorników

W przypadku przepływu laminarnego będziemy więc mieli $q_{12}=C \cdot (h_1-h_2)$ , a w przypadku przepływu turbulentnego $q_{12}=C \cdot \sqrt{h_1-h_2}$ . W tym drugim przypadku, musimy przy tym założyć, że $h_1>h_2$ – w przeciwnym wypadku przepływ $q_{12}=-C \cdot \sqrt{h_2-h_1}$ (jest ujemny, ponieważ skierowany w stronę przeciwną, niż wskazuje strzałka na rysunku). Takie zastrzeżenie nie jest potrzebne przy opisie przepływu laminarnego (dlaczego?).

Ponieważ układ składa się z dwóch zbiorników, potrzebne są dwa równania – po jednym dla każdego z nich. Zakładając, że np. wszystkie przepływy są laminarne równania opisujące dynamikę takiego układu przyjmują następującą postać:

$A_1\frac{dh_1}{dt}=q_{we}-C_1(h_1-h_2)$ ,

$A_1\frac{dh_1}{dt}=C_1(h_1-h_2) - C_2 h_2$ .

Trzeba pamiętać, że milcząco przyjęliśmy całkiem sporo założeń. Po pierwsze, zakładamy, że ciecz, wpływająca z góry do zbiornika, w zasadzie od razu rozkłada się po całej powierzchni (pomijamy efekty falowania). Po drugie, założyliśmy, że ciecz nie przelewa się przez ściany (czyli zbiorniki są wystarczająco wysokie dla założonych przepływów wejściowych). Wreszcie, po trzecie, założyliśmy, że przepływy są cały czas albo turbulentne, albo laminarne. Po czwarte – nic nie kapie…

Jeśli wpis Ci się spodobał i uważasz, że może warto, by Twoi znajomi go przeczytali – proszę poleć go.

Opisujemy układy – poziom I (elektryczne)

Kategoria 2 – proste układy elektryczne

Dynamikę układów elektrycznych będę przybliżał za pomocą obwodów, złożonych z trzech podstawowych elementów: rezystora, kondensatora i cewki, oraz dwóch typów źródeł: źródła prądowego i napięciowego (przy czym w przypadku źródeł wykorzystane zostaną symbole, zwykle rezerwowane dla źródeł prądu/napięcia stałego – u mnie będą niekoniecznie stałe):

Zależności pomiędzy natężeniem prądu a spadkiem napięcia na tych elementach, są następujące:

Dla rezystora (prawo Ohma):
$u_R=R \cdot i_R$

Dla kondensatora:

$i_C=C \cdot \frac{du_C}{dt}$

Dla cewki:

$u_L=L \cdot \frac{di_L}{dt}$

Istnieją elementy, dla których zależności pomiędzy prądem i napięciem są bardziej skomplikowane, ale na razie nie będę się nimi zajmował.

Zajmijmy się stworzeniem opisu dla poniższego układu:

Najpierw, spróbujmy wykorzystać wszystkie zależności pomiędzy natężeniami prądów i napięciami:

$u_{R1}=R_1 i_1$ ,
$u_{R2}=R_2 i_L$

$u_L=L\frac{di_L}{dt}$

$i_C=C\frac{du_C}{dt}$

oraz prawa Kirchoffa:

$i_L=i_1+i_C$

$u_C=u_{R1}$

$u=u_{R1}+u_L+u_{R2}$

Jak widać, mamy siedem niewiadomych: $i_1(t)$ , $i_C(t)$ , $i_L(t)$ , $u_C(t)$ , $u_L(t)$ , $u_{R1}(t)$ i $u_{R2}(t)$ , i siedem równań – czyli opis jest kompletny. Posługiwanie się nim byłoby jednak niewygodne, stąd zwykle redukujemy liczbę równań i zmiennych, stosując podstawienia z jednego równania do kolejnych. W zależności od tego, jak chcemy ustandaryzować formę opisu, posługiwać się będziemy albo układem dwóch równań pierwszego rzędu (tzn. bez pochodnych wyższych rzędów):

$i_L=\frac{u_C}{R_1}+C\frac{du_C}{dt}$

$u=u_C+L\frac{di_L}{dt}+i_L R_2,$

co, po uporządkowaniu wyrażeń, stanowi tzw. równania stanu (o czym w osobnym wpisie). Możemy opis sprowadzić do pojedynczego równania różniczkowego wyższego rzędu, np. wstawiając do drugiego z powyższych równań zależność określającą $i_L$ z pierwszego równania:

$u=LC\frac{d^2 u_C}{dt^2}+\left( \frac{L}{R_1}+R_2C \right)\frac{du_C}{dt}+\left(1+\frac{R_2}{R_1} \right) u_C.$

Postępując w sposób opisany powyżej (tzn. uwzględniając prawa Kirchhoffa i zależności pomiędzy natężeniem prądu i napięciam na poszczególnych elementach) możemy opisać dowolny układ elektryczny, a równania końcowe są bilansami prądów i napięć.

Jeśli wpis Ci się spodobał i uważasz, że może warto, by Twoi znajomi go przeczytali – proszę poleć go.

Układy dynamiczne – wprowadzenie

Ponoć jeden obraz zastępuje tysiąc słów – to niech będą dwa tysiące:

Układ dynamiczny – to taki, którego zachowanie, opisane pewnymi wielkościami, zmienia się w czasie. Może nas interesować tylko końcowy efekt (coś, co będzie dalej nazywane stanem ustalonym), ale jeśli naprawdę mamy mówić o dynamice układów, to końcowy efekt będzie jedynie drobnym elementem rozważań, a główny nacisk będzie położony na sposób dochodzenia do stanu ustalonego (bądź na brak takowego stanu).

W powyższym zdaniu chyba się zagalopowałem – trudno się wyzwolić z okowów języka akademickiego. Spróbujmy inaczej. Wyobraźmy sobie, że mamy do czynienia z prostym podajnikiem, który po włączeniu powinien coś podnieść na zadaną wysokość (uwaga: przykład maksymalnie uproszczony, tak by łatwo można było sobie wyobrazić, co przedstawia poniższy wykres – proszę się nie czepiać). W najprostszym modelu (żeby nie straszyć, schematu ani równań dla tego przykładu nie będzie) wejściem (sterowaniem) jest siła, jakiej należy użyć, a wyjściem – wysokość, na jaką udało się podnieść nasz ciężar. Oczywiście, im ciężar większy, tym większej siły należy użyć. Urządzenie jest tak skonstruowane, że po jego włączeniu (zadaniu stałej siły na wejściu), po pewnym (najlepiej krótkim) czasie podajnik osiąga pewną stałą wysokość i jego położenie przestaje się zmieniać (ustala się – stąd nazwa „stan ustalony”).

Pierwsze pytanie, jakie należy zadać, brzmi: „Jak dużą siłą powinniśmy zadziałać?”. Załóżmy, że potrafimy odpowiedzieć na to pytanie. To jednak nie wystarczy, by można było ogłosić sukces. W zależności od tego, jakie elementy zostały wykorzystane do konstrukcji podajnika, jego położenie może w różny sposób dążyć do wymaganej przez nas wartości ustalonej (patrz rysunek poniżej).

Rys. 3 Trzy przebiegi sygnału wyjściowego, otrzymane dla różnie dobranych parametrów układu. Wszystkie dążą do takiego samego stanu ustalonego, jednak w różny sposób. Linia czerwona reprezentuje przebieg, który można byłoby uznać za niezadowalający, ze względu na długi czas potrzebny do osiągnięcia stanu ustalonego. Linia niebieska reprezentuje odpowiedź układu, który jest znacznie szybszy, ale pojawiają się w nim oscylacje, które mogą być nie do zaakceptowania. Linia czarna mogłaby zostać uznana jako zadowalająca odpowiedź układu.

I tu dochodzimy do pierwszego z celów zajmowania się dynamiką układów – zdobycia umiejętności przewidywania, jak układ się zachowa w odpowiedzi na konkretne wymuszenie i wykorzystania tej wiedzy w projektowaniu układów (w tym doborze elementów składających się na układ). Patrzymy przy tym na różne cechy takich układów – na pierwszy rzut skupmy się na (chyba) najbardziej oczywistych :

Jak szybko układ dojdzie do stanu ustalonego (trzeba to jeszcze zdefiniować – np. po jakim czasie wartość wyjścia będzie się utrzymywać w przedziale +/-5% wartości stanu ustalonego?

Czy w układzie pojawią się oscylacje, czy też układ będzie dążył do stanu ustalonego bez oscylacji („aperiodycznie”)?

Jak duże przeregulowania pojawią się na wyjściu?

Rys. 4 Aperiodyczna odpowiedź układu. T_ust oznacza czas umownie przyjęty jako czas niezbędny do osiągnięcia stanu ustalonego

Rys. 5 Oscylacyjna odpowiedź układu. T_ust oznacza czas umownie przyjęty jako czas niezbędny do osiągnięcia stanu ustalonego

Oczywiście, można dochodzić do odpowiedzi na te pytania metodą prób i błędów – ale chyba lepiej najpierw trochę policzyć, zasymulować, a dopiero potem budować prototyp układu, który chcielibyśmy sprzedać za duże pieniądze… Zwłaszcza, że metoda prób i błędów może sporo kosztować…

Jak już wiemy, jak układ zareaguje na konkretne wymuszenia, możemy przejść do następnego etapu – jak kształtować sterowanie, żeby układ zachowywał się dokładnie w taki sposób, jakiego od niego oczekujemy. Przykładowo, jeśli mamy do czynienia z robotem, który ma przenieść w poziomie element z jednego miejsca na drugie, to pytanie brzmi: Jak sterować silnikami, które poruszają poszczególnymi członami robota? A jeśli chcemy naładować akumulator samochodu elektrycznego – to jak zmieniać napięcie (natężenie prądu) w urządzeniu ładującym, żeby to zrobić w najkrótszym czasie?

Problem w tym, że nawet jeśli to my skonstruowaliśmy układ, to jego parametry znamy jedynie z pewną dokładnością. Ponadto, jak pokażę w kolejnych wpisach, model, umożliwiający udzielenie odpowiedzi na zadane powyżej pytania, jest zawsze uproszczonym opisem rzeczywistości. W dodatku, na układ, oprócz naszego sterowania, mogą oddziaływać jeszcze zakłócenia. W związku z tym, staramy się sterować nie w układzie otwartym (tak jak na Rys. 1), ale w torze zamkniętym, wykorzystując informację z urządzeń pomiarowych do tego, aby osiągnąć pożądany efekt:

Rys. 6 Najprostszy schemat zamkniętego układu sterowania

A to już jest automatyka… Do której kiedyś dojdziemy… Ale też życie:

Jeśli wpis Ci się spodobał i uważasz, że może warto, by Twoi znajomi go przeczytali – proszę poleć go.

O czym? Dla kogo? Po co?

Od jakiegoś czasu obserwuję, że to, co dla mnie oczywiste, niekoniecznie musi być oczywiste dla innych (zresztą każdy tak ma). Moja Babcia mawiała: „Nie pamięta wół, jak cielęciem był”. Postaram się o tym pamiętać – dlatego czasami wpisy mogą się wydawać zbyt podstawowe. Chciałbym jednak dotrzeć nie tylko do swoich, ale również do innych studentów, którzy mogą bazować na innych podstawach, a także do wszystkich, którzy w duszy mają ukrytego inżyniera, który do rozwinięcia skrzydeł potrzebuje odrobiny zrozumienia układów, z którymi ma do czynienia. Może się nawet okazać, że niektóre wpisy będą miały wartość dla absolutnie-nie-mam -w-sobie-nic-z-inżyniera osób 🙂

Treści, zawarte we wpisach bloga będą dotyczyły układów dynamicznych, ich opisu, różnych punktów widzenia, z których można na nie spoglądać. Pojawią się konkretne przykłady (początkowo bardzo proste, żeby nie powiedzieć prymitywne – ale tylko idąc od prostych przykładów, możemy zrozumieć te bardziej skomplikowane), tak by każda czytająca to osoba mogła sobie wyobrazić o czym mowa i powiązać wzory, wykresy, z zachowaniem układu. Będę dążył do tego, by wpisy były zrozumiałe dla każdego, kto chce zrozumieć, co się dzieje, a nie tylko zapamiętać wzór i po zdaniu egzaminu (kartkówki, kolokwium itp.) natychmiast zapomnieć.

Jako przykłady posłużą mi proste układy mechaniczne, elektryczne i „hydrauliczne”. Wychodzę z założenia, że każdy kiedyś coś przelewał z jednego pojemnika do drugiego (może nawet przez lejek), popychał coś albo obracał, włączał żarówkę – stąd takie, a nie inne przykłady. Jak dobrze pójdzie, to od takiego włączania żarówki przejdziemy do odłowu łososi w hodowli w norweskim fiordzie…

Będzie też seria wpisów w serii ipocomito („i po co mi to?”, tzn., dlaczego warto się uczyć algebry, analizy, logiki i innych groźnie wyglądających rzeczy) – może bardziej dla potencjalnych, niż aktualnych studentów (ale kto wie?).

Układy dynamiczne – czyli takie, których zachowanie, opisane pewnymi wielkościami (przesunięcie masy, prędkość, natężenie prądu, napięcie, objętość cieczy w zbiorniku, temperatura, stężenie jakiejś substancji, liczba komórek nowotworowych, ilość dostępnej gotówki, poziom zadowolenia itd., itp., itd), zmienia się w czasie.

Dlaczego zrozumienie dynamiki jest ważne, jak można je wykorzystać – o tym w następnym wpisie.

Dlaczego powstał blog? Chyba głównie, żeby rozładować moją chęć uczenia wszystkich o wszystkim… Na wykładach zwykle nie ma czasu, żeby mówić o „podstawach podstaw” – bo nie zdążyłbym przejść do meritum przed końcem semestru. Do tego wynudziłbym te osoby, które podstawy znają. Mam nadzieję, że dzięki lekturze moich wpisów przynajmniej część z Was zdobędzie motywację do nauki i do poznawania mechanizmów, które na nas wszystkich wpływają (to już wyszło bardzo górnolotnie).

Póki co, wersja uboga. Skupię się na treściach wpisów. Mam nadzieję, że z biegiem czasu również wygląd strony będzie ułatwiał łatwiejsze dotarcie z treścią do czytelnika