Opisujemy układy – poziom I (zbiorniki)

Ostatnim typem układów, które będą służyły do ilustrowania różnych zagadnień, związanych z dynamiką układów, są układy zbiorników. Najprostszy z nich wygląda tak:

Wejściem w tym układzie jest przepływ $q_{we}$ . Zależy ono tak naprawdę od ciśnienia wejściowego i charakterystyki oraz stopnia otwarcia zaworu, ale dla uproszczenia posługiwać się będziemy właśnie przepływem. Równania dla zbiorników oparte są na bardzo prostej regule – różnica między ilością cieczy wpływającej i wypływającej ze zbiornika stanowi przyrost objętości cieczy w tym zbiorniku:

$\frac{dV}{dt}=q_{we} - q_{wy}$ .

Zakładając, że pole przekroju powierzchni zbiornika jest stałe i wynosi $A$ , otrzymujemy

$A\frac{dh}{dt}=q_{we} - q_{wy}$ .

Możemy mieć do czynienia z jednym z dwóch typów przepływów: laminarnym albo turbulentnym. W przepływie laminarnym wielkość przepływu jest proporcjonalna do ciśnienia panującego w zbiorniku, a ponieważ ciśnienie jest proporcjonalne do wysokości słupa cieczy, możemy zapisać

$q_{wy}=C \cdot h$ ,

gdzie $C$ jest współczynnikiem proporcjonalności.

W przepływie turbulentnym wielkość przepływu jest proporcjonalna do pierwiastka z ciśnienia, co można zapisać jako

$q_{wy}=\hat{C} \cdot \sqrt{h}$ .

Ostatecznie, dynamika zmian objętości cieczy/wysokości słupa cieczy/przepływu wyjściowego jest opisana za pomocą jednego równania różniczkowego i jednego równania algebraicznego. Sprowadzając ten zapis do pojedynczego równania różniczkowego, np. w przypadku przepływu turbulentnego, otrzymujemy:

$A\frac{dh}{dt}=q_{we}- \hat{C} \cdot \sqrt{h}$ .

W przypadku, gdy przekrój zbiornika nie jest stały, obliczenia nieco się komplikują. Przykładowo, gdy zbiornik ma kształt lejka:

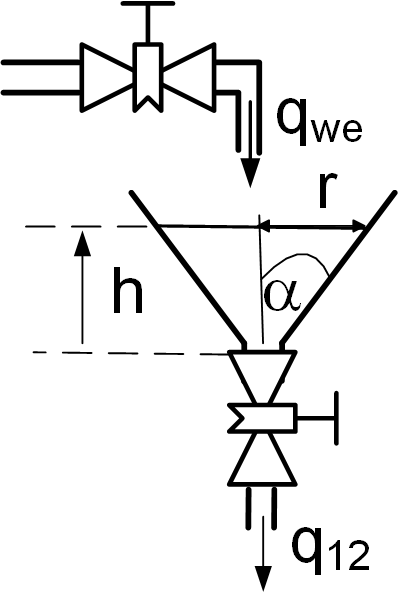
jego objętość można obliczyć jako objętość stożka (zaniedbujemy fakt, że tak naprawdę jest to stożek ścięty), czyli

$V=\frac{1}{3}\pi r^2 h$ .

Pamiętając o tym, że $h=h(t)$ i $r=r(t)$ , oraz uwzględniając zależność $r=h\tan \alpha$ , otrzymujemy $V=\frac{1}{3}\pi \tan^2\alpha h^3$ i możemy obliczyć zmianę objętości $V$ w czasie jako

$\frac{dV}{dt}=\pi \tan^2\alpha h^2 \frac{dh}{dt}$ .

W takim razie, dynamika zmian poziomu cieczy w zbiorniku opisana jest równaniem

$\pi \tan^2\alpha h^2 \frac{dh}{dt}=q_{we}-q_{wy}$ ,

gdzie $q_{wy}$ , w zależności od typu przepływu, jest opisany jedną z wyżej podanych zależności algebraicznych.

W przypadku, gdy mamy do czynienia z dwoma połączonymi zbiornikami, jak na rysunku poniżej, przepływ pomiędzy nimi zależy od różnicy ciśnień (co sprowadza się do zależności od różnicy poziomów cieczy).

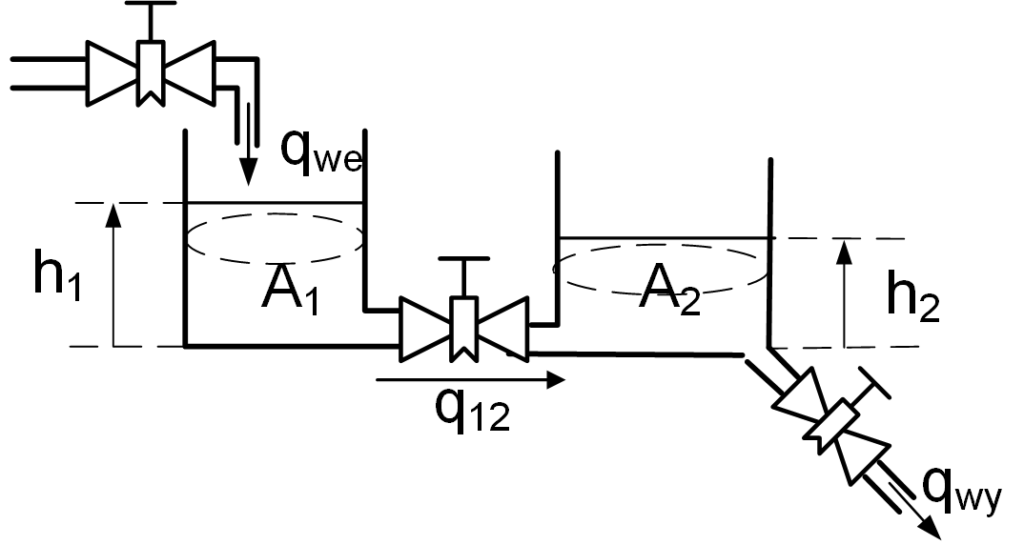
Rys. 3 Układ dwóch połączonych zbiorników

W przypadku przepływu laminarnego będziemy więc mieli $q_{12}=C \cdot (h_1-h_2)$ , a w przypadku przepływu turbulentnego $q_{12}=C \cdot \sqrt{h_1-h_2}$ . W tym drugim przypadku, musimy przy tym założyć, że $h_1>h_2$ – w przeciwnym wypadku przepływ $q_{12}=-C \cdot \sqrt{h_2-h_1}$ (jest ujemny, ponieważ skierowany w stronę przeciwną, niż wskazuje strzałka na rysunku). Takie zastrzeżenie nie jest potrzebne przy opisie przepływu laminarnego (dlaczego?).

Ponieważ układ składa się z dwóch zbiorników, potrzebne są dwa równania – po jednym dla każdego z nich. Zakładając, że np. wszystkie przepływy są laminarne równania opisujące dynamikę takiego układu przyjmują następującą postać:

$A_1\frac{dh_1}{dt}=q_{we}-C_1(h_1-h_2)$ ,

$A_1\frac{dh_1}{dt}=C_1(h_1-h_2) - C_2 h_2$ .

Trzeba pamiętać, że milcząco przyjęliśmy całkiem sporo założeń. Po pierwsze, zakładamy, że ciecz, wpływająca z góry do zbiornika, w zasadzie od razu rozkłada się po całej powierzchni (pomijamy efekty falowania). Po drugie, założyliśmy, że ciecz nie przelewa się przez ściany (czyli zbiorniki są wystarczająco wysokie dla założonych przepływów wejściowych). Wreszcie, po trzecie, założyliśmy, że przepływy są cały czas albo turbulentne, albo laminarne. Po czwarte – nic nie kapie…

Jeśli wpis Ci się spodobał i uważasz, że może warto, by Twoi znajomi go przeczytali – proszę poleć go.

Opisujemy układy – poziom I (zbiorniki)

Dodaj komentarz

Anuluj pisanie odpowiedzi